Difference between revisions of "AY1516 T2 Team Hew - Prediction"
m |
|||
| Line 36: | Line 36: | ||
== <p style="font-family:Trebuchet MS; border-left: 6px solid #62b762; padding-left:10px; line-height:40px; height:40px"><b>Claim Amount Distribution Fitting</b></p>== | == <p style="font-family:Trebuchet MS; border-left: 6px solid #62b762; padding-left:10px; line-height:40px; height:40px"><b>Claim Amount Distribution Fitting</b></p>== | ||
=== Analyze Distribution=== | === Analyze Distribution=== | ||
| − | Vaughn (1996) and a number of actuaries have mentioned that | + | Vaughn (1996) and a number of actuaries have mentioned that Claim amounts have to factor in inflation for greater accuracy. However, as the highest inflation rate attained by Indonesia for the time period of study is about 7%, this is rather negligible. Using JMP Pro 12, we first excluded rows where Claim amount = 0 and derived the distribution statistics of: |
<br /> | <br /> | ||
{| class="wikitable" style="text-align: center; width: 70%; margin-left: auto; margin-right: auto; border: none;" | {| class="wikitable" style="text-align: center; width: 70%; margin-left: auto; margin-right: auto; border: none;" | ||
| Line 58: | Line 58: | ||
<br /><br /> | <br /><br /> | ||
We can see that -2Log(Likelihood) is minimized with the LogNormal distribution. According to JMP Pro documentation, maximum likelihood estimation is used in determining the parameters for the LogNormal distribution. Naturally, we can see why the LogNormal distribution derives the lowest -2Log(Likelihood) as the problem of maximizing the likelihood function is reformulated to become a minimization of the negative of the natural logarithm of the likelihood function. | We can see that -2Log(Likelihood) is minimized with the LogNormal distribution. According to JMP Pro documentation, maximum likelihood estimation is used in determining the parameters for the LogNormal distribution. Naturally, we can see why the LogNormal distribution derives the lowest -2Log(Likelihood) as the problem of maximizing the likelihood function is reformulated to become a minimization of the negative of the natural logarithm of the likelihood function. | ||
| − | + | <br /> | |
We did another Goodness-of-Fit test using Kolmogrov’s D test with the null hypothesis as “H0: The data is from the LogNormal Distribution”, thus obtaining a D-statistic of 0.048569 and a p-value of 0.01. As p-values are the probability of getting an even more extreme statistic given the true value being tested is at the hypothesized value (usually at zero), a small p-value means that the statistic is unlikely to be that extreme by coincidence. In this case, the p-value of 0.01 is fairly small, indicating significance that the fitted distribution is LogNormal. | We did another Goodness-of-Fit test using Kolmogrov’s D test with the null hypothesis as “H0: The data is from the LogNormal Distribution”, thus obtaining a D-statistic of 0.048569 and a p-value of 0.01. As p-values are the probability of getting an even more extreme statistic given the true value being tested is at the hypothesized value (usually at zero), a small p-value means that the statistic is unlikely to be that extreme by coincidence. In this case, the p-value of 0.01 is fairly small, indicating significance that the fitted distribution is LogNormal. | ||
| − | + | <br /> | |
Using JMP Pro’s Diagnostic Plot function, we can visually affirm the goodness-of-fit, as seen in the figure below. The actual Claim amount is plotted against its corresponding estimated LogNormal probability on the Y-axis. We can see that most of the data points fall on the Line of Fit (red line) for Claim amounts within the mid-range, thus depicting a good fit. | Using JMP Pro’s Diagnostic Plot function, we can visually affirm the goodness-of-fit, as seen in the figure below. The actual Claim amount is plotted against its corresponding estimated LogNormal probability on the Y-axis. We can see that most of the data points fall on the Line of Fit (red line) for Claim amounts within the mid-range, thus depicting a good fit. | ||
<br /><br /> | <br /><br /> | ||
[[File:Quantile_plot.png|center|Diagnostic Plot]] | [[File:Quantile_plot.png|center|Diagnostic Plot]] | ||
<br /><br /> | <br /><br /> | ||
| − | + | Several other papers have adopted to fit Claim amounts with the LogNormal distribution because of its right-skewed shape (Adeleke, Ibiwoye), and this is in line with our findings. We therefore fit a LogNormal distribution to the Claim amounts, which allows us to use it for prediction or modelling purposes. | |
| + | <br /><br /> | ||
| + | ===Segmentation=== | ||
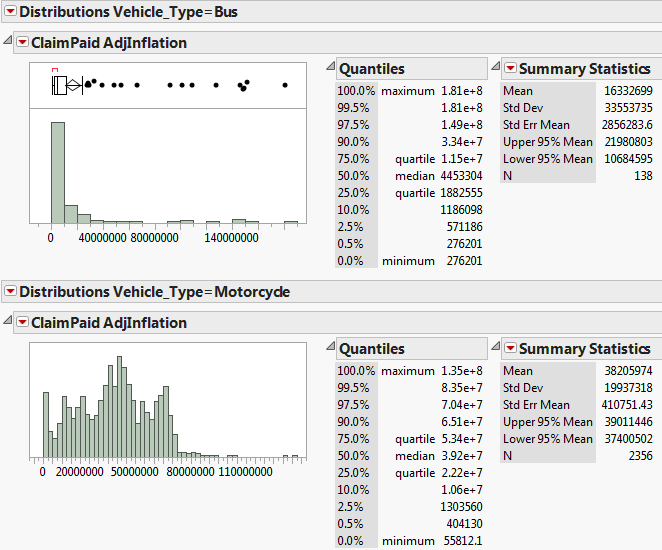
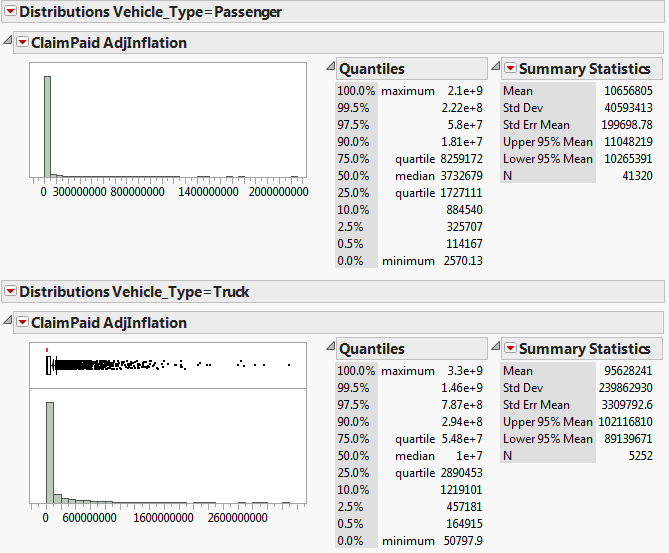
| + | We hypothesized that there would be differences in claim amounts for different vehicle types, due to the varying costs of each vehicle, so we proceeded to segment the dataset by the Vehicle Type (Passenger Car, Bus, Truck, Motorcycle) and plot the Claim amount distributions for each segment: | ||
| + | <br /><br /> | ||
| + | [[File:Segment1.png|center|Claim amounts for Bus & Motorcycle]] | ||
| + | <br /> | ||
| + | [[File:Segment2.png|center|Claim amounts for Passenger Car & Truck]] | ||
| + | <br /><br /> | ||
| + | We can see that the distribution shape for Motorcycles is different as compared to the other Vehicle Types, as about 90% of the claims were theft-related. The other Vehicle Types have a similar right-skewed distribution which we can fit a LogNormal distribution, albeit with different parameter values due to the differences in Claim amounts. Claim amount is generally higher for larger Vehicle Types. | ||
</div> | </div> | ||
Revision as of 10:57, 17 April 2016
| Exploratory Analysis | Prediction |
Contents
Claim Amount Distribution Fitting
Analyze Distribution
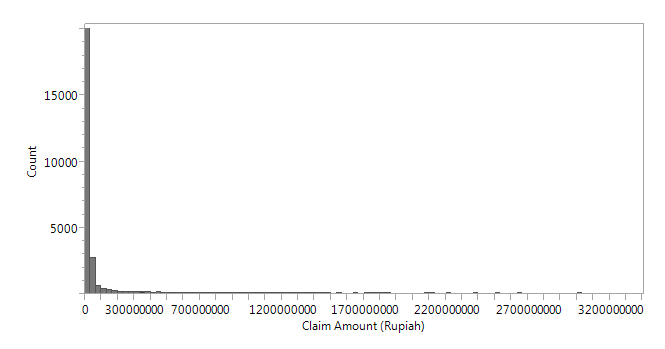
Vaughn (1996) and a number of actuaries have mentioned that Claim amounts have to factor in inflation for greater accuracy. However, as the highest inflation rate attained by Indonesia for the time period of study is about 7%, this is rather negligible. Using JMP Pro 12, we first excluded rows where Claim amount = 0 and derived the distribution statistics of:
| N | Min | Max | Median | Mean | Standard Deviation |
|---|---|---|---|---|---|
| 49,066 | 2,570 | 3,295,056,701 | 4,297,418 | 21,090,896 | 90,927,485 |
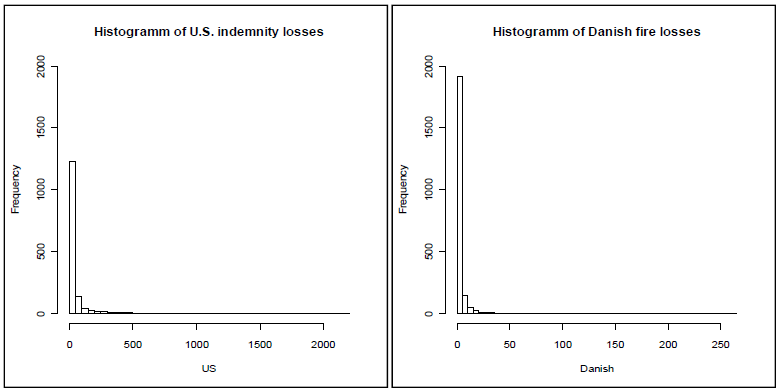
From figure above, we can see that there are many instances of small claim amounts, with few instances of extreme values, and the distribution shape is right skewed. Similar distribution shapes for Claim amounts have also been derived from insurance companies based in other regions, as seen in figure below taken from Eling’s research (2011).
Fit Distribution
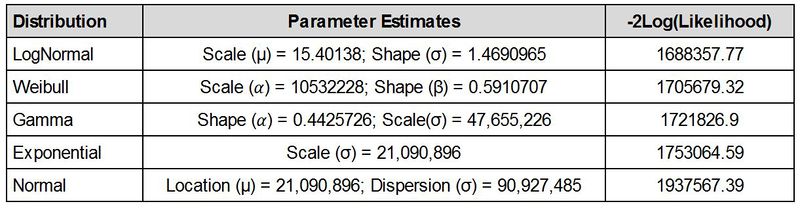
We then attempt to fit several distributions on the Claim amounts column, using JMP Pro’s Fit Distribution function. The most suitable distribution selected will be the one which minimizes the -2Log(Likelihood), taken to be a measure of variation or uncertainty in the sample.
We can see that -2Log(Likelihood) is minimized with the LogNormal distribution. According to JMP Pro documentation, maximum likelihood estimation is used in determining the parameters for the LogNormal distribution. Naturally, we can see why the LogNormal distribution derives the lowest -2Log(Likelihood) as the problem of maximizing the likelihood function is reformulated to become a minimization of the negative of the natural logarithm of the likelihood function.
We did another Goodness-of-Fit test using Kolmogrov’s D test with the null hypothesis as “H0: The data is from the LogNormal Distribution”, thus obtaining a D-statistic of 0.048569 and a p-value of 0.01. As p-values are the probability of getting an even more extreme statistic given the true value being tested is at the hypothesized value (usually at zero), a small p-value means that the statistic is unlikely to be that extreme by coincidence. In this case, the p-value of 0.01 is fairly small, indicating significance that the fitted distribution is LogNormal.
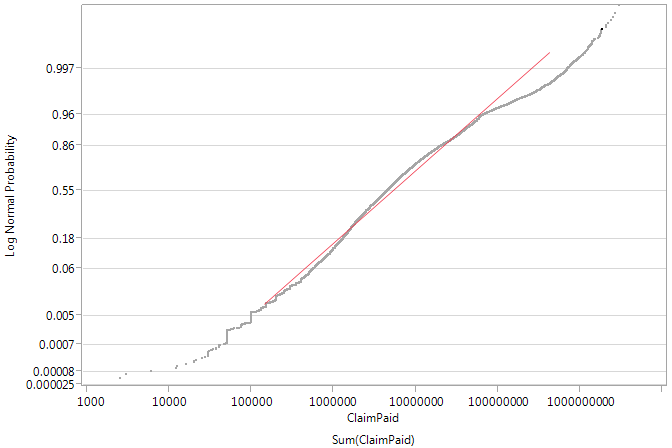
Using JMP Pro’s Diagnostic Plot function, we can visually affirm the goodness-of-fit, as seen in the figure below. The actual Claim amount is plotted against its corresponding estimated LogNormal probability on the Y-axis. We can see that most of the data points fall on the Line of Fit (red line) for Claim amounts within the mid-range, thus depicting a good fit.
Several other papers have adopted to fit Claim amounts with the LogNormal distribution because of its right-skewed shape (Adeleke, Ibiwoye), and this is in line with our findings. We therefore fit a LogNormal distribution to the Claim amounts, which allows us to use it for prediction or modelling purposes.
Segmentation
We hypothesized that there would be differences in claim amounts for different vehicle types, due to the varying costs of each vehicle, so we proceeded to segment the dataset by the Vehicle Type (Passenger Car, Bus, Truck, Motorcycle) and plot the Claim amount distributions for each segment:
We can see that the distribution shape for Motorcycles is different as compared to the other Vehicle Types, as about 90% of the claims were theft-related. The other Vehicle Types have a similar right-skewed distribution which we can fit a LogNormal distribution, albeit with different parameter values due to the differences in Claim amounts. Claim amount is generally higher for larger Vehicle Types.
Linear Regression
Coming Soon
Research & Methodology
Coming Soon
References