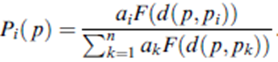Qui Vivra Verra - Project Findings
Further analysis of the data set can be accomplished through market segmentation. The concept of k-means clustering can be applied on the Transaction Dataset, with the clustering parameters set as:
- Recency (number of days from last transaction to end of the FY)
- Frequency (number of transactions performed within the FY)
- Monetary (average number of books borrowed per transaction)
Each patron will then be assigned to a cluster, with each cluster homogeneous within and heterogeneous across. From here, we can determine the dominant cluster of library member that each library caters to – which can provide some operational insights by understanding the demographics of the bulk of each library’s patrons.
An adaptation of the Huff’s Model (Huff, 1964) will be applied in the analyses.
To quote a paper by Okabe & Sugihara (2012):
To state a general form of the Huff model, we consider a space S (which may be a plane or a network), in which n stores are located at p1, …, pn. Let ai be the attractiveness of store i, which may be a function of its floor area, the number of items sold, its parking area and so forth; let d(p, pi) be the distance between a point p on S and the store at pi, which may be the Euclidean distance or the shortest-path distance; and let F(d(p, pi)) be a monotonically decreasing function of d(p, pi), referred to as a distance decay function or distance deterrence function. In these terms, the Huff model showing the probability of a consumer at p choosing the store at pi is generally written as:
Adapting the Huff’s Model to the context of our project, we would consider Singapore as space S, in which n libraries are located at p1, …, pn. Let ai be the attractiveness of library i, which is estimated by a multinomial generalised linear regression equation, taking into account the following factors (non-exhaustive):
- Size of the library’s collection
- Gross floor area of the library
- Type of facility the library is located in (i.e. mall, stand-alone etc)
- Size of facility the library is in (i.e. if the library is located in a mall, this refers to the gross floor area of the mall)
- Number of MRT stations within a set distance (to be determined) from the library
- Number of bus stops within a set distance (to be determined) from the library
- Number of bus routes within a set distance (to be determined) from the library
- Opening hours of the library
- Number of educational institutes (i.e. primary/secondary schools, junior colleges, polytechnics, ITE, universities) within a set distance (to be determined) from the library
- Number of other libraries (only considering the list under NLB) within a set distance from the library
Let d(p, pi) be the distance between an area (geographical subzone) p on S and the library at pi, which may be the Euclidean distance or the shortest-path distance; and let F(d(p, pi)) be a monotonically decreasing function of d(p, pi), referred to as a distance decay function or distance deterrence function. Therefore, the above-stated formula can be interpreted as the probability of a consumer at p choosing the library at pi.
Dividing the number of patrons in each subzone at p that visited a library pi by the total number of patrons in the subzone at p, we can obtain a probabilistic model which estimates the proportion of time that a patron from subzone p will visit library i in any given FY. Then, by substituting the known values of ai (to be determined by the regression model) and d(p, pi) into the adapted Huff’s Model, we are able to derive possible values of the power parameter (∝) that govern the distance decay function. By doing this process iteratively, we can obtain an unbiased estimate for ∝ that is accurate to a certain significant level.