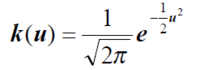Kiva Project Findings Final
| Interim | Final |
|---|
Contents
Area of study
The bulk of its loans, in terms of both amount and quantity, are funded in the Philippines, thus being the country of focus in our analysis. The Republic of Philippines is made up of 7107 tropical islands, having a total square area of 300,000km2 and being 65% mountainous (Net Industries, 2018). Although the country’s official languages are Filipino (Tagalog) and English, it is a country that has diverse regional cultures, with three languages serving as regional lingua francas: Ilokano in Northern and Central Luzon, Tagalog in Central and Southern Luzon, and Cebuano in the Visayas and Mindanao.
Philippines are divided into three major island groups: Luzon, Visayas, and Mindanao.
Luzon, the most populous and largest island in the Philippines, home to the country’s capital and major metropolis Manila. It leads the country in agriculture and industrial manufacturing, and more than half of the Filipino population lives on Luzon (Britannica). Luzon also consists of Palawan Island, a large island southwest of Manila.
Visayas is an island group located in the centre of Philippines. It consists of seven large islands and several hundred smaller ones, and the region is famous for agriculture and fishing (Britannica).
Mindanao is the second largest main island after Luzon. The island has narrow coastal plains, with broad, fertile basins and extensive swamps(Britannica). Mindanao has the strongest Muslim presence in Philippines amongst the three islands, whose dominant religion is Roman Catholic, and is home to most of the ethnic minorities. Agriculture is a key industry like other islands, while its textile and timber industries are also important due to deposits of raw materials.
With vast ethnic, cultural, economic and religious differences between various provinces, geospatial analysis is used to identify how do Kiva’s loan attributes differ across the Philippines.
Analysis
Kernel Density Analysis
Methodology
Kernel density function is a non-parametric method of estimating the probability density function (PDF) of a continuous random variable, and is non-parametric as the underlying distribution for the variable is not assumed. Each sample point will have its own weight function which represents its influence of the density values in the surrounding neighbourhood, and each ‘bump” is centred at the datum and spreads out symmetrically to cover the neighbouring values. The size of the “bump” represents the probability assigned at the neighbourhood of values around that datum, and the estimated model is the summation of all the kernel function “bumps”.
The Gaussian Kernel function, represent by k(u), follows a normal distribution curve to represent the intensity of different points. The density plot for the Gaussian function for Philippines is plotted below.
Figure 1: Screenshot of loan_themes_by_region.csv
Findings
Spatial Autocorrelation Analysis
Methodology
Spatial autocorrelation measures a correlation of a variable with itself through space. In Kiva’s context, a positive spatial autocorrelation indicates that similar borrowing patterns appear in neighborhood regions while negative spatial autocorrelation suggests that dissimilar borrowing patterns appear in neighborhood regions. In order to find out whether nearby geo-locations demonstrate similar loaning patterns, a spatial autocorrelation analysis is adopted to study the geographical distribution of the number of loans for different sectors. (Celebioglu, F. and Dall'erba, S., 2010)
First, we need to define neighborhood, the area surrounding target locations. During the analysis, the number of loans for one location will be compared with its neighbors so that a statistical conclusion about whether neighborhood area are correlated with each other can be drawn. Therefore, the criteria for selecting neighbors is of great importance and will largely affect the analysis results.
Spatial weight measures the intensity of relationships between different spatial units. In this study, spatial weight matrix will be applied to establish neighborhood structure and choosing appropriate weight matrix will be the main focus of this study. There are two basic approaches to construct a spatial weight matrix: contiguity based weight matrix and distance based weight matrix.
Contiguity Based Method (Queen)
A prerequisite for adjacency based weight matrix is that two areas can be considered as neighbours only if they share a common border. In the queen method, sharing only one boundary point will be considered neighbours as well. The queen contiguity weights are defined in the following formula. A weightage of 1 in the matrix means the nearby location neighbour with the target location while 0 means that nearby location is not an adjacent neighbour. (Andy Mitchell, 2005)
Distance Based Method
Another way to calculate the spatial weight is based on the actual distance between two centroids of geographical area.
1. K Nearest Neighbor Method K is a user defined variable. The neighbours for a specific spatial unit are selected based on the distance and K. The KNN weights are calculated based on the following formula. Nk(i)represents a list of K nearest neighbor for spatial unit i. If spatial unit j falls under this list, a weightage of 1 is assigned to it. Otherwise, 0 is assigned.
2. Inverse Distance Weighting Based Method Inverse Distance Weighting (IDW) makes the assumption that the influence of a spatial unit on other area will decrease as the distance increase. Thus, nearer neighbor will be assigned heavier weight. The inverse distance weight is calculated based on the following formula. dij denotes the distance between geolocation i and j. In this study, we assume 𝛼 equals to 1. (Smith, T, n.d.)
Row Standardization
After establishment of the neighborhood structure, we will standardize the weight matrix by assigning a proportional weight to each neighbor location based on the total number of neighbors for that target location. The row standardization will be applied to minimize the influence of unequal number of the neighbors. However, the row standardization will not be applied to inverse distance weight matrix. If the neighbor units are very close to or even at the same location as the target spatial unit, row standardization will assign an dominant weight to the neighbors regardless of those relatively distant object, which will distort the result. (Andy Mitchell, 2005)
Local Indicator For Spatial Association (LISA)
Local Indicator for spatial association (LISA) is a kind of statistics which measures the extent to which similar values are clustered together. (Luc Amelin, n.d.) Local Moran I is used as a LISA statistics in this study to determine the significant level of clustering results and the formula used is as shown below. wij denotes the weight between geolocation i and j. xi and xj denotes the target value in region i and j. X bar represents the mean value across different areas.
A large positive value for Iiindicates that the similar values appeared in the neighborhood region while the negative value indicates that dissimilar values appeared in the adjacent regions. (Andy Mitchell, 2005)
Findings
Reference
1. Net Industries. (n.d.). Philippines - History Background. Retrieved April 01, 2018, from http://education.stateuniversity.com/pages/1197/Philippines-HISTORY-BACKGROUND.html http://histclo.com/country/oce/phl/phl-reg.html
2. Celebioglu, F. and Dall'erba, S (2010) "Spatial disparities across the regions of Turkey: an exploratory spatial data analysis", Annals of Regional Science, Vol. 45, No. 2, p. 379-400
3. Yu, D and Wei (2008) "Spatial data analysis of regional development in Greater Beijing, China, in a GIS environment", Papers in Regional Science, Vol 87, No. 1, pp 97-117
4. Elias, M and Rey, S.J. (2011) "Educational Performance and Spatial Convegence in Peru
5. Andy Mitchell,(2005), The ESRI Guide to GIS Analysis: Volume 2: Spatial Measurements & Statistics,”, p. 136-145 http://region-developpement.univ-tln.fr/fr/pdf/R33/Elias.pdf
6. Luc Amelin,(n.d.). Local Indicators of Spatial Association-LISA, Retrieved from https://onlinelibrary.wiley.com/doi/pdf/10.1111/j.1538-4632.1995.tb00338.x
7. Smith, T. (n.d.). Spatial Weight Matrices. Retrieved April 08, 2018, from: https://www.seas.upenn.edu/~ese502/lab-content/extra_materials/SPATIAL%20WEIGHT%20MATRICES.pdf
8. Britannica. (2016, October 03). Mindanao. Retrieved April 08, 2018, from https://www.britannica.com/place/Mindanao
9. Britannica. (2016, October 03). Visayan Islands. Retrieved April 08, 2018, from https://www.britannica.com/place/Visayan-Islands
10. Roxas, N.R. & Fillone, A.M. Transportation (2016) 43: 661. https://doi-org.libproxy.smu.edu.sg/10.1007/s11116-015-9611-4
11. Philippine Statistics Authority: CountrySTAT Philippines, 2018. Retrieved on 15 April 2018 from http://countrystat.psa.gov.ph/