Automotive Angels - Methodology
Contents
Methodology
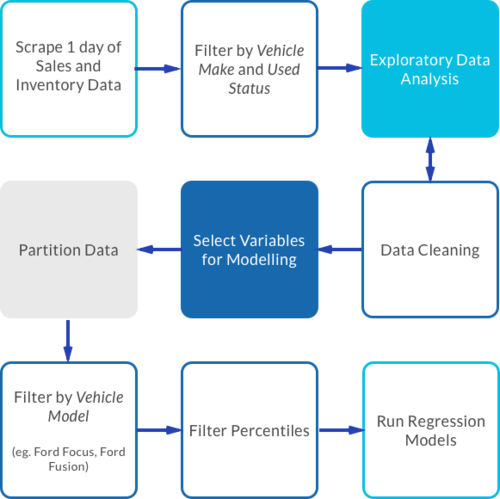
Figure 3: Process Flow Overview
- Scrape 1 day of Sales and Inventory Data from various online car dealers provided by our sponsor company.
- Filter “Vehicle Make” to BMW. We also filtered out cars that are new, where “Used Status” equals 0.
- Understanding the data using exploratory data analysis for each “Vehicle Make”.
- Data Cleaning which involves filtering extreme outliers, handling missing values, variable creation and correcting discrepancies. This is done in parallel to exploratory data analysis.
- Select variables for modelling to remove multicollinearity and remove unnecessary variables.
- Data partition dataset into 60% training data and 40% test data.
- Filter to the highest frequencies of “Vehicle Model” in each “Vehicle Make”.
- Filter out the bottom 10% and top 10% of each “Vehicle Model”
- Run each regression model on each “Vehicle Model” and choose the best performing one.
Linear Regression
Linear Regression is commonly used to predict a continuous outcome and is a powerful tool for analyzing data. This paper focuses on variable selection - choosing the best subset of predictors. This is to remove redundant predictors, reduce noise and reduce effects of collinearity. In the business sense, we can save time and money by not measuring redundant predictors. Backward regression starts with all the predictors in the model, and removes the predictor with the highest p-value greater than what we set as the industry widely accepted value of 0.5. Then we refit the model until when all p-values are less than the critical value. As for forward selection, it works in the reverse order where it starts with no variables in the model, and predictors with the lowest p-value less than the critical value is added until no new predictors can be added. We also explored the combination of backward and forward selection, known as stepwise regression. This addresses the situation where the situation where variables are added or removed early in the process. Stepwise procedures are relatively cheap computationally but there are some drawbacks: (1) due to the one-at-a-time of adding or dropping variables, it is possible to miss the optimal variable (2) variables that are dropped can still be correlated with the target variable, it is just that they provide no explanatory effect beyond those variables already included in the model. This paper also considers the method of least absolute shrinkage and selection operator (LASSO), a regression analysis method that performs both variable selection and regularization to enhance prediction accuracy and interpretability of the statistical model. The LASSO method is similar to the forward regression algorithm except that it does not add the predictor into the model directly. The coefficient is increased until predictor is no longer the one most correlated with residual. It starts off with all predictor variables of coefficient zero, and find the predictor that is most correlated with the target variable. The lasso is useful as it allows choosing the number of predictors to use in the regression model.
Model criterion
In SAS Enterprise Miner, cross validation errors are calculated from the Training data set. One observation is omitted one at a time and model is re-estimated with the remaining observations. The re-estimated model is then used to predict the value of the target for the omitted observation. In the case of a continuous target, the error is the squared difference between the actual and predicted variables. While we have sufficient data used in our regression model, in specific cases we may have smaller set of data and hence we used cross validation error criterion for model criterion selection within each node.
Model Selection
The question of model selection is frequently visited in analytics. Given the wide choices of criterion such as AIC, cross-validation, R2, stepwise procedures, some are algorithms for choosing a useful model while others are criteria for judging the quality of a model, how do analytics practitioners choose? A method that is coherent and general enough to handle problems is desired. In this paper, we chose to optimize root mean squared error (RMSE), and selected predictors based on the cross-validation error instead of adjusted R2. This is largely influenced by the ease of business use where RMSE offers a specific price margin from the pricing model.
Application of Regresison
Figure 4: Selection of Tables into Final Metadata Data is obtained through crawling of individual dealership websites and other service providers such as autotrader.com and edmunds.com. About 30,000,000 rows, approximately 6GB of data is obtained each day and appended to the database. The data is saved on MySQL Database and stored on S3 on Amazon Web Services as a .csv file. To ensure the accuracy and completeness of the results, the entire dataset was extracted without sampling. Figure 4 shows the list of variables that are crawled each day and stored in the Vehicle Inventory and Sales table. Another dataset given by the client which includes the updated latitude, longitude, dealer city and state. Hence, we used the updated variables such as Dealer City, Dealer State, and Dealer Longitude and Latitude as displayed under the Dealer table as seen in Figure 4. Also, through research, we could found the cost of owning a car across the different states in United States as seen in State Car Cost table. From our dataset, we also created other variables such as “Vehicle Model Age” which is derived from subtracting Model Release Year from 2017. We rolled up various vehicle models into 4 main vehicle categories. Also, from the dealer longitude and latitude, we could derive variables such as “Number of Similar Cars in 50 miles, in 100 miles and Number of Dealers in 50 miles and in 100 miles”.
Data Preparation
We will be carefully studying the dataset to understand each variable and prepare them for analysis. The steps for cleaning the data are as follows: 1. Recording the description and range and summary statistics for each variable 2. Identifying outliers 3. Identifying duplicate fields 4. Identifying missing and invalid values 5. Transform skewed variables if it affects modelling accuracy 6. Create new variables to increase modelling accuracy 7. Documentation of all step The data table contains a total of 41 million records, where each record represents a single car. To ensure accuracy and completeness of result, the entire dataset was extracted without sampling. The following Extract, Transform and Load (ETL) process was carried out on the selected tables, as shown below.
Missing Values
We removed the rows which have missing values of “Current Selling Price” since that is the target variable. Without data from the target variable, the row would be unable to be used in the model. We have decided to remove the “Current Selling Price” individually from the 3 makes, which reduces the load on the system due to the large dataset. Hence, we will be split the tables into three different Vehicle Makes: BMW, Ford and Chevrolet. For all 3 Vehicle Makes, removing the rows without a “Current Selling Price” helps reduce the percentage of missing data for rows significantly (Figure 27, Figure 30, Figure 33). From Figure 27, Figure 30 and Figure 33, we can see that the percentage of missing values for all numerical variables are greatly reduced after we removed data points which do not have the Current Selling Price. With 52,998, 2,820,534 and 2,344,860 rows left after the reduction, we still had sufficient data to create an accurate prediction model.
Removing Outliers
We removed outliers from “Vehicle Mileage” and “Current Selling Price”. We removed extreme outliers that are 3 times more than the interquartile range from tail quantiles of 0.1.
Removing Discrepancies
Vehicle Model
In our data, the “Vehicle Model” column has some discrepancies with some rows adding the vehicle trim or in various forms of capitalization. We have cleaned each “Vehicle Make” differently because each “Vehicle Make” has different types of labelling errors. The formulas that we used to correct the “Vehicle Model” column and distributions can be found in the appendix at Figure 34, 35, and 36. The new column after correction is named “Corrected Vehicle Model”. Vehicle model names were based on the official list by the different car makes, BMW, Ford and Chevrolet. Chevrolet and Ford were more difficult to clean due to the larger number of variations, hence using “Contains” function in the formula helped to reduce the work needed.
| Vehicle Make | Number of Vehicle Models | Number of Corrected Vehicle Models |
|---|---|---|
| BMW | 41 | 27 |
| Ford | 174 | 59 |
| Chevrolet | 265 | 82 |
Vehicle Category
Since our scope was used cars, we needed to exclude vehicles that were not considered to be cars. In BMW, there were motorbikes while Ford and Chevrolet included vans and trucks. As such, we looked up each model online and categorized each model into “Car” or “Not Car” under the “Vehicle Category” column. The formulas for each “Vehicle Make” can be found in the appendix at Figure 43, 44, 45. In other words, if the “Vehicle Model” is a car model, it would be labelled as “Car”. If not, it would be labelled as “Not Car” in the new column, “Corrected Vehicle Model”.
Variable Creation
Number of Dealers in 50/100 miles
From our primary data, we collected from our interviews, we found out that the furthest someone will go to get a car that they have in mind is 100 miles. As such, from our dataset, we wanted to create a variable which would consider this competition from other dealers. To measure competition, we counted the number of dealers and the total number of similar cars in a 50 and 100-mile radius. Using a python script, we looked at each dealer and its surrounding dealers within a 50 and 100-mile radius. For example, surrounding Dealer A is only Dealer B which is 20 miles away and Dealer C which is 56 miles away. The output of “Dealers in 50 miles radius” would be 1 and the output of “Dealers in 100 miles radius” would be 2. Python libraries that we used include pandas, numpy and geopy. If you would like to have a closer look at the script, the python script is called createNearSimilarCars.py and will be attached to the submission of this report.
Number of Similar Cars in 50/100 miles
As said in the previous section, another way to measure competition is to count the number of cars of the same model that is sold by nearby dealers. This could be a better measurement since a nearby dealer that does not have a car a customer wants would not be a direct competitor. Using a python script, we looked at each car model and counted the number of similar cars in other dealers within a 50 or 100-mile radius. For example, if there is a Ford Fusion being sold in Dealer A, the script would count the number of Ford Fusions in a 50 mile and 100-mile radius in other dealers. Let say there is Dealer B which is 20 miles away and has 3 Ford Fusions for sale while Dealer C is 75 miles away and has 5 Ford Fusions for sale. The output would be 3 for the “Number of Similar Cars in 50 miles” while the output would be 8 for the “Number of Similar Cars in 100 miles”. Similarly, python libraries that we used include pandas, numpy and geopy. If you would like to have a closer look at the script, the python script is called createNearSimilarCars.py and will be attached to the submission of this report.
Car Cost Category by State
We hypothesized that the cost of car maintenance differs from each state and this will affect consumers’ preferences on used cars. (known by secondary research) Upon further investigation, we found out that there is a significant difference in terms of insurance cost, car tax between each state. Collectively, they affect the car cost by a large extent. Using $25,000 as the cost of an average car in US, we can retrieve the cost of car maintenance for 3 years for each state from a finding done by Huffington Post. This variable is named “3 Years Car Cost”.
Figure 4: Binning Visualization on JMP for “3 Years Car Cost” We then binned the variable to assign a categorical variable, “Car Cost Category by State”, to each state which tells us how expensive it is to own a car compared to other states. There are 4 categories of car maintenance cost as seen in Figure 4: Low ($8000 – $10000), Average ($10000 – $12000), High ($12000 – $14000), Very High ($14000 – $16000). After creating a table of states which are binned into these 4 categories, we do an inner join with the primary data set which includes the used car sales data.
Vehicle Model Age
An older vehicle model would be likely command a lower price. For example, a 2010 BMW 3 Series would be likely to fetch a lower price than a 2012 BMW 3 Series. Therefore, we decided to take this into consideration by finding out the vehicle model’s age. To calculate this, we took the current year, 2017, and subtracted the “Vehicle Model Year” and created a new column called “Vehicle Model Age”.
Rolling Up Car Category
Our initial aim is to create a predictive model that is generalised enough and applicable to all models, and there were 27 models. As our objective is to create a generalised model There were too many levels, n=27, in a single factor such as “Vehicle Model”. Consequently, we tried aggregating the levels in “Car Category” and roll up the 27 models into the common 4 car types: ‘SUV’, ‘Sports car’, ‘MPV’, ‘Economy car’, ‘Sedan’.
Figure 5: Frequency of Clean Vehicle Category
Figure 6: Difference in backward regression results between generalised vehicle categories and vehicle model specific for BMW
However, the results show that such classifications while general produced a huge margin of error of 6000 while the vehicle model specific variation had an RMSE of 3000. Upon discussion with our client, we prioritized in choosing the smallest value of RMSE and hence subsequent models are done with specific models.
Modelling
In the modelling process, we explored a series of regression methods – stepwise, backwards, forwards and LASSO to test which regression method gives us the best prediction. After which, we would document our steps and analysis for our client to develop a more comprehensive model and integrate it into their system.
Model Preparation – Using 10th-90th Percentile of Data
In attempt to create a generalized model, we experimented with BMW and rolled up car models into 4 supersets and removed the top and bottom of 25% of Current Selling Price. However, the errors were too high. Hence, it suggest that creation of a generalized model may not be suitable and we filtered down each Car Make, BMW in this case, into their respective Car Models. In each model, we classified the top 10% and bottom 10% of “Current Selling Price” as outliers and excluded them in our analysis using Enterprise Miner. After which, we created a regression equation for each model which will be explained in greater detail later in this report.
Figure 12: Current Selling Price for various Models
Variable Creation
Main variable(s) excluded for regression analysis: Vehicle Make - We will be focusing on BMW, Ford and Chevrolet separately for this category Vehicle Trim - Since Vehicle Trim a subset of Vehicle Model and there are too many levels in this factor for analysis, Cleaned Vehicle Model will be considered instead Main variable(s) included for regression analysis: Vehicle Mileage - Effects of depreciation on price Selection of other variables can be found under Variables selection table can be found from Figure 64 under appendix.
Model Selection
As the target variable is a numerical continuous variable, hence regression would be a more suitable modelling technique to predict the price. We will be exploring the following regression methods: ● Forward Regression ● Backward Regression ● Stepwise ● LASSO Initially, we explored various objectives to best optimize the model. We tried a few indicators such as Adjusted R2, RMSE or cross validation error. Having the lowest RMSE as the model objective made the most business sense as the client can immediately have a good sense on the possible error range of the model. We first performed all the methods of regressions mentioned on BMW but left out LASSO for subsequent “Vehicle Makes” because LASSO performed significantly poorer than the other methods.